Throughout most of last quarter and this quarter you investigated situations in which an object moves with a constant acceleration because the force(s) acting on the object is constant. A very special kind of motion occurs when the force exerted on an object varies linearly with the object's position. If this force always acts in a direction opposite to the displacement of the object, then a repetitive back-and-forth motion results. This motion is called periodic or oscillatory motion.
You are familiar with many objects that vibrate or oscillate -- a tuning fork, the balance wheel of a mechanical watch, a pendulum, a plastic ruler held firmly over the edge of a table and gently struck, the strings of a guitar or piano. Spiders detect prey by the vibrations of their webs, cars oscillate up and down when they hit a bump, and buildings and bridges vibrate when heavy trucks pass or the wind is strong. Electrical oscillations occur in radios and TV sets. At the atomic level, atoms vibrate within molecules, and the molecules of a solid oscillate about their equilibrium positions.
In this lab you will study the oscillatory motion of springs that are either vertically suspended with a mass, or attached to a glider on an air track. You will use different methods to determine the spring constants of different spring configurations, and compare the oscillation frequency of different spring and mass configurations. You will also explore an oscillating spring system in which a resistive force considerably damps the motion, and an oscillating spring system that moves in response to forces applied at different frequencies.
OBJECTIVES: After successfully completing this laboratory, you should be able to:
PREPARATION:
Read Fishbane, Gasiorowicz, and Thornton: Chapter 13
Before coming to lab you should be able to:
PROBLEM #1: MEASURING SPRING CONSTANTS
You are selecting light-weight springs for a large antique
clock, and you need to determine the spring constant of the
springs.
| What is the spring constant of the spring? |
Since the spring constant must be known accurately for the clock
to keep time, you decide to take two independent measurements of
the spring constant. One method is a straight forward application
of Hooke's' Law, where you will determine the ratio between the
hanging mass and the displacement of the mass from its
equilibrium position. For the second method you measure the
period of oscillation of a vertically suspended spring-mass
system.
EQUIPMENT
| You will hang a spring from a ring stand and use a meter stick to measure how far the spring stretches. You also have a mass holder, an assortment of masses, a triple-beam balance, and a stopwatch. |
PREDICTIONS
1. Predict quantitatively the spring constant of a spring from measurements of the displacement of different masses hung on the spring.
2. Predict quantitatively the spring constant of a spring from measurements of the period of oscillation of a mass attached to the spring.
METHOD QUESTIONS
To complete your predictions, it is useful to apply a problem-solving strategy such as the one outlined on page 35 of your text:
Method #1: Suppose you hang several different known
masses on a spring and measure the vertical displacement of each
mass.
1. Make two sketches of the situation, one before you attach a
mass to a spring, and one after a mass is suspended from the
spring and is at rest. Draw a coordinate system and label the
equilibrium position (where the spring is unstretched), the
stretched position, the suspended mass, and the spring constant.
Assume the springs are massless.
2. Draw a force diagram of a hanging mass at rest. Label
the forces. Use Newton's second law and Hooke's law to write the
equation of motion for the hanging mass. Solve this equation for
the spring constant.
3. Use your equation to sketch the expected shape of the graph of
displacement (from the equilibrium position) versus mass for the
mass-spring system. How is the slope of this graph related to the
spring constant?
Method #2: Suppose you hang a mass from the spring,
start it oscillating, and measure the period of
oscillation.
1. Make a third sketch (next to the two sketches above) of the
oscillating spring/mass system at a time when the mass is below
its rest position. Identify and label this new position on the
same coordinate axis.
2. Draw an additional force diagram of the mass at this new
position. Label the forces.
3. Apply Newton's laws and Hooke's law, and write the equation of
motion for the mass when it is at its rest position, and at the
new position (below the rest position).
When the mass is below its rest position, how is the total
stretch of the spring from its equilibrium position ([[Delta]]y)
related to the stretch to its rest position ([[Delta]]y1) and the
additional stretch to its new position ([[Delta]]y2).
4. Solve your equations for acceleration as a function of the
suspended mass, the spring constant, and the displacement of the
mass from its rest position ([[Delta]]y2). Compare your equation
to equation 13-15 in your text.
5. Compare your equation for acceleration to equation 13-8. Based
on this comparison, predict the angular frequency of the system
as a function of the suspended mass and the spring constant. How
is the angular frequency related to the period of oscillation?
EXPLORATION
Method #1: Select a series of masses that give a usable range of displacements. (Note: The assumption of massless springs holds when the suspended mass used to stretch the springs is about 500 grams.) Decide on a recording scheme that allows you to measure consistently the displacement of each mass. Decide how many and which measurements you will need to make to determine the spring constant.
Method #2: Secure the spring safely to the stand and select a mass that gives a good, crisp oscillation without excessive wobbling. Why is this important? Practice starting the mass in motion smoothly. Why is this important? Which is most important, how you start the oscillating motion, or the consistency in the method of starting the motion? Why?
Decide how to measure accurately the period of oscillation of the mass-spring system. How can you minimize the error introduced by your reaction time in starting and stopping the stopwatch? How many times should you measure the period to get a reliable value?
MEASUREMENT
For both methods, make the measurements that you decided you needed to determine the spring constant.
Analyze your data as you go along so you can decide how many measurements you need to make to determine the spring constant accurately and reliably.
ANALYSIS
Method #1: Draw a graph of displacement versus mass for the mass-spring system. From the slope of this graph, calculate the value of the spring constant, including the uncertainty.
Method #2: Calculate the spring constant and the uncertainty in its value from your measurements of the oscillating system.
CONCLUSION
How do the two values of the spring constant compare? Which method has the highest precision? Which method is quicker? Which method do you feel is the most reliable? Justify your answers.
PROBLEM #2: THE EFFECTIVE SPRING CONSTANT
| What are the spring constants of
two single springs that would replace the side-by-side
and end-to-end spring configurations? |
Outline your measurement plan.
PROBLEM #3: OSCILLATION FREQUENCY WITH TWO SPRINGS
| What is the frequency of the
oscillating glider? |
You will use an air track, the adjustable end stop, two springs and a stopwatch.
Predict quantitatively the frequency of the simple harmonic motion of the glider.
2. Draw force diagrams of the oscillating glider. Label the forces.
3. Apply Newton's laws and write the equation of motion for the glider.
Calculate the frequency (with uncertainty) using your Prediction equation.
How does your measured frequency compare with your predicted frequency?
If you completed Problem 2: What is the effective spring constant of this configuration? How does it compare with the effective spring constants of the side-by-side and end-to-end configurations?
PROBLEM #4: OSCILLATION FREQUENCY OF AN EXTENDED SYSTEM
| Will the motion of the actors
change if the heavier stunt man is used instead of Bruce
Willis?. |
2. Draw force diagrams of the oscillating glider and hanging mass. Label the forces.
3. Apply Newton's laws and write the equations of motion for the glider and the hanging mass.
Determine the best range of hanging masses to use.
Graph the frequency versus the hanging mass. On the same graph, show your predicted relationship.
EXPLORATORY PROBLEM #5: DAMPED OSCILLATIONS
You notice that your seismic detector (from Problem 3) is a little too sensitive and you would like the oscillations to end quicker. You know from your exploration with the apparatus that adding masses to the glider does not help, so you E-mail your physics professor for help. Your professor suggests that you hang magnets on the glider. The message goes on to explain that magnets in motion produce currents in nearby metals, so the system loses energy to the metal (in this case the air track). This is an example of an effect called "damping." Your professor assures you that if there is time, you will learn more about damping next quarter. Not entirely convinced, you decide to experiment with it yourself.
| How does hanging magnets on the glider affect the
oscillating motion of the glider? |
EQUIPMENT
You will use your seismic detector apparatus from Problem 3, but you will also have some ballast masses and a collection of ceramic magnets (about the size of a half-dollar) with a hole in their centers. These ring-magnets are placed on the glider, using the same posts used to support the ballast masses.

PREDICTION
The damping effect that the magnets will have on the oscillator can be quantified by measuring the number of cycles (oscillations) that it takes for the amplitude of the system to drop to one-half its initial value. We will call this quantity the "half-amplitude" of the damped system.
Make an educated guess about how you think the half-amplitude of the damped system will depend on the number of magnets you hang on the glider. Will the half-amplitude increase, decrease, or stay the same as the number of magnets increases? What do you expect the graph of half-amplitude versus the number of magnets to look like?
EXPLORATION
Find the best place for the adjustable end stop on the air track. DO NOT STRETCH THE SPRINGS PAST 40 CM OR YOU WILL DAMAGE THEM, but stretch them enough so the glider oscillates smoothly.
Do the magnets stick to the air track? To the glider?
Explore what happens as you add magnets to the glider. Does the number of cycles it takes for the system to reach half-amplitude depend on the initial amplitude?
Determine a consistent way to measure the half-amplitude of the system, and practice counting the number of cycles.
As you increase the mass of the glider (using the ballast masses, not the magnets), what happens to the frequency of the oscillation? What happens to the half-amplitude?
Outline your measurement plan.
MEASUREMENT
Measure the half-amplitude when there are no magnets on the glider. Repeat the measurement each time you add a magnet to the glider. How will you determine the uncertainty in your measurements?
ANALYSIS
Make a graph of the half-amplitude versus the number of magnets on the glider.
CONCLUSION
How does the half-amplitude of the damped system depend on the number of magnets you hang on the glider? Did your measured graph agree with your predicted graph? If not, why not? State your result in the most general terms supported by your analysis?
What could be some other uses of this phenomenon?
EXPLORATORY PROBLEM #6: DRIVEN OSCILLATIONS
You are now prepared to calibrate your seismic detector (from Problem 3 and Problem 5). You need to determine how the amplitude of the oscillations of the detector will vary with the frequency of the earthquake aftershocks. So you replace the end stop on the air track with a device that moves the end of the spring back and forth, simulating the earth moving beneath the air track. The device, called a mechanical driver, is designed so you can change its frequency of oscillation.
| How will the amplitude of the oscillations vary with
frequency? |
EQUIPMENT
You will use your seismic detector apparatus, the ring magnets to damp the oscillations, and a mechanical driver.

The mechanical driver is somewhat like a loudspeaker with one end of a metal rod attached to the center, and the other end of the rod is attached to one of the springs. The driver is connected to a signal generator which causes the rod to oscillate back and forth with adjustable frequencies which can be read off the display on the signal generator.
PREDICTION
Make your best-guess sketch of what you think a graph of the amplitude of the glider versus the frequency of the mechanical driver will look like. Assume the driver has an amplitude of a few millimeters.
EXPLORATION
Examine the mechanical driver. Find a way of mounting it at the end of the air-track, using the clamp and metal rod. Mount the driver so its shaft is aligned with the glider's motion. Connect it to the signal generator, using the output marked Lo (for ``low impedance''). Use the smallest amplitude which is sufficient to observe the oscillation of the glider at the lowest frequency possible.
Determine the accuracy of the digital display on the frequency generator by timing one of the lower frequencies.
Devise a scheme to accurately determine the amplitude of a glider on the air track, and practice the technique.
MEASUREMENT
If you do not know the natural frequency of your system, determine this frequency (see Problem 3).
Collect enough glider amplitude and driver frequency data to test your prediction. Be sure to collect several data points near the natural frequency of the system.
ANALYSIS
Make a graph the oscillation amplitude of the glider versus driver frequency. Is this the graph you had anticipated? Where is it different? Why? What are the limitations on the accuracy of your measurements and analysis?
CONCLUSION
Can you explain your results? Is energy conserved? What will you tell your boss about your design for a seismic detector?
1. The diagram below shows an oscillating mass/spring system at times 0, T/4, T/2, 3T/4, and T, where T is the period of oscillation. For each of these times, write an expression for the displacement (x), the velocity (v), the acceleration (a), the kinetic energy (KE), and the potential energy (PE) in terms of the amplitude of the oscillations (A), the angular velocity ([[omega]]), and the spring constant (k).

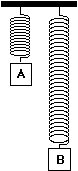
| 2. Identical masses are attached to identical springs
which hang vertically. The masses are pulled down and
released, but mass B is pulled further down than mass A,
as shown at right. a. Which mass will take a longer time to reach the equilibrium position? Explain. b. Which mass will have the greater acceleration at the instant of release, or will they have the same acceleration? Explain. c. Which mass will be going faster as it passes through equilibrium, or will they have the same speed? Explain. d. Which mass will have the greater acceleration at the equilibrium point, or will they have the same acceleration? Explain. |
 |
| 3. Two different masses are attached to different springs which hang vertically. Mass A is larger, but the period of simple harmonic motion is the same for both systems. They are pulled the same distance below their equilibrium positions and released from rest. |  |
a. Which spring has the greater spring constant? Explain.
b. Which spring is stretched more at its equilibrium position?
Explain.
c. The instant after release, which mass has the greater
acceleration? Explain.
d. If potential energy is defined to be zero at the equilibrium
position for each mass, which system has the greater total energy
of motion? Explain.
e. Which mass will have the greater kinetic energy as it passes
through its equilibrium position? Explain
f. Which mass will have the greater speed as it passes through
equilibrium? Explain.
| 4. Five identical springs and three identical masses
are arranged as shown at right. a. Compare the stretches of the springs at equilibrium in the three cases. Explain. b. Which case, a, b, or c, has the greatest effective spring constant? The smallest effective spring constant? Explain. c. Which case would execute simple harmonic motion with the greatest period? With the least period? Explain. |
 |