The Piecewise Diffusion of the Silicon Dimer
We present a detailed view of the diffusion of silicon dimers on the silicon (001) surface. Through a combination of atom-tracking and ab initio modeling, the dimer is shown to move one atom at a time rather than as a two-atom unit. The details of the pathway depend on the diffusion channel: On top of dimer rows, the two atoms of a dimer separate but remain bound during diffusion. In the troughs between dimer rows, the two atoms separate completely and move independently before rejoining in a new location.
Since the 1960’s, techniques for imaging with atomic resolution have provided us a remarkable look at the variety of ways in which atoms and small molecules move on surfaces. The advent of the scanning tunneling microscope (STM) in the 1980’s has allowed the extension of atomic-scale diffusion studies to a broad range of systems involving both metal and semiconductor surfaces. A new technique for directly measuring surface diffusion, called "atom-tracking" improves the time resolution of the STM. By this method, the STM tip is locked onto and follows through individual diffusive hops. Here, we discuss new atom-tracking studies and ab initio calculations which produce a significant advance in our understanding of dimer diffusion on Si(001), revealing piecewise diffusion pathways.
The Si(001) surface consists of parallel rows of dimer bonds which are the result of pairs of surface atoms binding together in order to reduce the overall surface energy. These dimer rows are separated by 7.7 Å, and the spaces in between them are called troughs. Rows and troughs are distinct one-dimensional diffusion channels for Si ad-dimers. Theoretical work has shown that a dimer is very likely to form whenever two monomers meet, since dimer formation requires no energy barrier beyond that of monomer diffusion [1,2]. Once formed a dimer is very strongly bound. The energy required to separate a dimer has been calculated to be 1.33 eV for dimers on top of dimer rows [2,3]. Energetically, the row sites are more favorable than trough sites [1,2,3,4,5]. However, the distribution of dimers occupying the two types of sites upon formation is kinetically determined: one third form on rows and two thirds form in troughs [6].
Fig. 2. One Dimensional Schematic of Barrier to Diffusion. Because of the strong anisotropy of the Si(001) reconstructed surface, diffusion is strongly one dimensional.
We first discuss results for diffusion along dimer rows.
Diffusion in this channel is activated just slightly above room
temperature. The animation of Fig. 1 shows the diffusion of a
dimer (the white spot near the center of the image.) As can be
seen in the animation, the dimer's motion is restricted to one
dimension, along the substrate dimer rows. Fig. 2 is a schematic
of the energy contour along a row. A thermal activation of ED is necessary for the dimer to hop
from one well to the next. Tracking a dimer as it diffuses across
a silicon surface allows the determination of dimer diffusion
activation energy by applying the Arrhenius relation. The average
hop rate is expected to follow the Arrhenius relation for a
thermally activated process: ![]() , where r is the rate, E and v are the activation energy and
attempt frequency, T is the temperature, and k is
Boltzmann’s constant.
, where r is the rate, E and v are the activation energy and
attempt frequency, T is the temperature, and k is
Boltzmann’s constant.
![]()
Fig. 3 Arrhenius plot for determining diffusion activation energy. According to the Arrhenius relation R=ve-ED/KT for any simple thermally activated process. By observing hop rates at several temperatures we are able to determine values for both the activation energy, ED, and the attempt frequency , v. Note: at low temperatures the tip induced diffusion rate becomes significant; this is responsible for the large diffusion rate observed at room temperature.
By taking transition rate measurements at different sample temperatures, the plot in Fig. 3 has been constructed. From the slope of this plot, an activation energy for dimer diffusion is found to be 1.09 ± 0.05 eV.
It is worth noting that while the hop rate is plotted logarithmically, the temperature is not, so the plot is relatively unforgiving of errors in temperature measurements. For this reason we performed a temperature calibration using the known melting point of indium and we employed an iterative temperature equilibration method for measuring sample temperature.
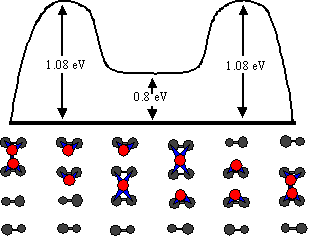
Fig. 4 Schematic diagram of the calculated diffusion pathway for row diffusion. These were constructed from the results of ab initio modeling by Yamasaki, Terakura, and Uda [2]. The pathway involves the dimer moving one atom at a time rather than as a unit. The dimer enters a weakly bound state as one atom moves ahead but remains together during diffusion.
In excellent agreement with our findings, Yamasaki, Terakura, and Uda found 1.08 eV by ab initio calculations for the diffusion pathway shown in Fig. 4.[2] While other processes were considered, including intact dimer diffusion, atomic exchange with the substrate (1.28 eV), and complete dissociation (1.6 eV), the piecewise path illustrated in Fig. 4 corresponds to the lowest energetic barrier. In addition to the good theoretical and experimental agreement on activation energies for diffusion, atom-tracking data also confirms that all hops during row diffusion are between adjacent sites along the row, as expected for the proposed pathway.
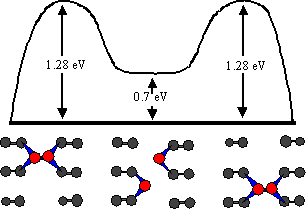
Fig. 5 Schematic diagram of the calculated diffusion pathway for trough diffusion. This was constructed from the results of ab initio modeling by Goringe and Bowler [7]. The pathway involves the dimer moving one atom at a time rather than as a unit. The dimer dissociates as one atom moves ahead, and the two atoms move up and down the trough independently until they meet again and reform the dimer in a new location.
We now report new atom-tracking results for trough diffusion, motivated by a recent ab initio study by Goringe and Bowler [7]. Goringe and Bowler propose that, as for row diffusion, trough diffusion requires the dimer to move one atom at a time, as shown schematically in Fig. 5. Although rather than remaining bound as the first atom moves ahead, the dimer completely breaks apart and its two atoms move nearly independently along the trough until they meet again and reform the dimer. This breaking apart is the costliest step energetically, with a calculated energy barrier of 1.28 eV [7]. The two atoms may come back together immediately after dissociating, as in Fig. 5. However, it is equally likely that they will move away from each other and continue to execute simultaneous one-dimensional random walks until they meet each other and reform the dimer. It is important to note that these single atom random walks occur on a much shorter time scale than the average time between breakup events, since the calculated energy barrier is much smaller, 0.6 eV compared to 1.28 eV [8]. Therefore, atom-tracking data should appear as instantaneous hops on the time scale that we observe. A simple statistical analysis results in the probability distribution for the dimer to reform a given number of sites away from its original site. Assuming no long-range interaction, Goringe and Bowler conclude that nearly 40% of the time the dimer reforms at its original site. The remaining dissociations result in observable hops, and the majority of the hops (71%) are expected to be between adjacent sites one spacing away. However, a significant fraction of hops are predicted to be longer than one spacing: 16% two, 6% three, and the rest more than three spacings. The presence or absence of these unusual long jumps in atom-tracking data provides a rather direct test of the proposed diffusion mode.

Fig. 6 Atom-tracking data at 433 ± 8 K. The position of the dimer was sampled at 100 Hz. The data are shown as displacement versus time both along the dimer row (top) and perpendicular to the dimer row (bottom). (The pause in the data near 1650 seconds was for imaging the area and verifying our identification of the dimer configuration). For the first 200 seconds, the dimer diffused rapidly on top of a dimer row, with an average hop rate of 3.4 Hz. Then, the dimer hopped sideways one spacing, into the trough. For the next 2150 seconds, the dimer hopped along the trough at a much slower rate of 6.5´ 10-3 Hz. Finally, the dimer hopped back onto the original dimer row and resumed rapid diffusion. The arrows point to three long hops of two spacings that occurred while in the trough.
Atom-tracking studies of trough diffusion confirm the presence of long jumps in this diffusion channel. Examples of this are shown in Fig. 3, a set of atom-tracking data at 433 K that demonstrates the possibilities for diffusion at higher temperatures [9]. In summary, this figure shows a dimer continuously tracked as it first diffuses on top of a dimer row, then hops sideways into a neighboring trough, diffuses along the trough, and finally hops back on top of the original dimer row. The arrows point to three long jumps of two spacings among a total of fourteen hops in the trough. It is striking how much slower diffusion in the trough is than diffusion on top of a dimer row. Using the statistical analysis described above, we find a value of 1.27 ± 0.08 eV for the energy barrier of trough diffusion. The calculated barrier of 1.28 eV is in close agreement with this value.
We have summarized our results for row and trough diffusion in Table 1. In each case, the observed hop length distribution is in good agreement with that expected according to whether theoretical modeling favors the dimer remaining bound or breaking apart during diffusion. The elevated percentage of single hops observed for trough diffusion may be attributed to a weak interaction between the atoms when they are only one site apart that results in a slightly enhanced probability for reforming the dimer.
Hop Length |
% Observed |
% If bound |
% If dissociated |
|
row diffusion (87 hops) |
||||
1 |
100 |
100 |
71 |
|
2 |
0 |
0 |
16 |
|
3 |
0 |
0 |
6 |
|
trough diffusion (73 hops) |
||||
1 |
85 |
100 |
71 |
|
2 |
12 |
0 |
16 |
|
3 |
3 |
0 |
6 |
|
Table 1. A tabulation of the measured hop length distributions for row and trough diffusion. These are compared to the distributions expected for two possibilities: when the dimer remains bound during diffusion and when the dimer dissociates during diffusion. We conclude that the dimer remains bound during row diffusion but dissociates during trough diffusion. These findings are in agreement with the results of theoretical modeling.
We have presented atom-tracking and ab initio studies that combine to reveal piecewise diffusion pathways for the Si dimer on Si(001). The dimer diffuses one atom at a time and not as a unit, becoming weakly bound (on the rows) or completely dissociating (in the troughs) during motion from site to site. The calculated channel-specific energy barriers are in excellent agreement with atom-tracking results. For diffusion in the trough, we observe long jumps spanning 2 and 3 lattice sites, a direct signature of the dimer’s dissociation and reformation during diffusion. In the future we expect atom-tracking to be applied to still more complex diffusion systems. For instance, it may be possible to follow changes in a large molecule’s position, orientation, and bonding as it moves along a surface.
1 T. Yamasaki, T. Uda and K. Terakura, Phys. Rev.
Lett. 76, 2949 (1996).
2 T. Yamasaki, T. Uda, and K. Terakura, Proceedings
of the Second Topical Meeting on Structural Dynamics of Epitaxy
and Quantum Mechanical Approach, Jan. 22-23, 1997, Kobe,
Japan, pp. 115-119. And communication with authors.
3 B. S. Swartzentruber, Phys. Rev. Lett. 76,
459 (1996).
4 G. Brocks and P. J. Kelly, Phys. Rev. Lett. 76
2362 (1996).
5 A. P. Smith and H. Jonsson, Phys. Rev. Lett. 77,
1326 (1996).
6 J. van Wingerden, A. van Dam, M. J. Haye, P. M. L. O.
Scholte, and F. Tuinstra, Phys. Rev. B. 55,
4723 (1997).
7 C. M. Goringe and D. R. Bowler, Phys. Rev. B 56,
R7073 (1997).
8 G. Brocks, P. J. Kelly, and R. Car, Phys. Rev.
Lett. 66, 1729 (1991).
9 M. Krueger, B. Borovsky, and E. Ganz, Diffusion
of Si dimers on Si(001) Surf. Sci. 385, 146 (1997).
We would like to thank the National Science Foundation for support under grant DMR-9614125. We would also like to thank T. Yamasaki, T. Uda, and K. Terakura for sharing their unpublished results with us, and C. Goringe and D. Bowler for helpful correspondence.
Jump to
Hot STM Labs
Diffusion
across rows
Copyright 1998 by the Regents of the University of Minnesota, Dept. of Physics & Astronomy. All rights reserved.