This laboratory will allow you to investigate the effect of interactions on the motion of objects. You can determine the motion of objects in response to diverse interactions by applying the force concept to each situation. In the first problem, you will investigate how surfaces effect the frictional force on a sliding object. The second problem illustrates the usefulness of the force concept and, in particular, the vector nature of forces, to a situation in which nothing is moving. In the next two problems you will investigate the usefulness and limitations of an approximate force law for frictional forces.
OBJECTIVES: After successfully completing this laboratory, you should be able to:
PREPARATION:
Read Fishbane, Gasiorowicz, and Thornton: Chapter 4, sections 1
through 3 and section 5; Chapter 5, sections 1 and 2. Review the
behavior of an object sliding down an inclined air track.
Before coming to lab you should be able to:
PROBLEM #1: HOW SURFACE EFFECTS THE KINETIC FRICTIONAL FORCE
You are helping a friend design a new game to use on the Midway at the Minnesota State Fair. The game is similar to shuffleboard -- players use a short stick to push a puck just hard enough so it will travel along a level surface and fall into one of several holes. To make the pucks and sliding surface, your friend wants to use old kitchen counter tops purchased cheap at a surplus store. One side of the material is composition board, and the other is a plastic laminate. He needs to know which surface, laminate or composition board, to use for the game. If there is too much friction no one will ever get the puck into the holes, and if there is too little friction then the game will be too easy and you will have to give too many prizes. He knows you are taking a physics course, so he asks you to help. To solve this problem, you devise and experiment to measure the coefficients of friction.
| |
What is the coefficient of kinetic friction between
the laminate surfaces and the composition board surfaces? |
EQUIPMENT
A disk is pulled along a level surface as shown below.
You can change the contact surface in two ways. You can flip the disk, which has both a wood side and a laminated side. Another way of changing the contact surface is to flip the board, which also has a wood side and a laminated side. The mass hanger (Object A) allows you to determine the force exerted on the disk by the string if you assume the pulley is frictionless and the string has a negligible mass. A spark tape running through a spark timer will allow you to record the motion of the disk as it slides.
PREDICTION
Examine the Table of Coefficients of Friction. Make your best guess of what you think the approximate values will be for the coefficient of friction of laminate on laminate and composition board on composition board. Explain your reasoning.
METHOD QUESTIONS
To test your prediction, you must determine how to calculate the kinetic frictional force from the quantities you can measure in this problem. It is useful to have an organized problem-solving strategy such as on page 35 (and 107, 110) in your text:
1. Make a sketch of the problem situation similar to the one in the Equipment section. Indicate the motion of the objects.
2. The "known" quantities in this problem are the mass (m) of the object A, the mass (M) of the disk, and the acceleration of the disk and object A. The unknown quantity is the kinetic frictional force on the disk.
3. Use Newton's laws to solve the problem. Draw separate force diagrams of object A and the disk after they start accelerating. (If you need help, see pages 107 and 110 in your text.)
4. For each force diagram, write Newton's second law and the corresponding equation of motion for each mass. What special condition connects the motion of the disk and Object A? (If you need help, see page 134.) Use Newton's third law to relate the force of the string pulling on the disk to the force of the string pulling on object A (assuming a "massless" string).
In this case, you should have four equations and four unknowns -- three force equations and one equation that relates the accelerations of the disk and object A.
5. Solve the four equations for the kinetic frictional force. Your equation determines how the frictional force on the disk depends on its mass (M), its acceleration (a), and the mass (m) of object A.
EXPLORATION
Find a range of masses for object A that allows the disk to accelerate across the board.
Try these masses for the two combinations of contact surfaces (laminate on laminate and composition board oncomposition board) to be sure the disk accelerates uniformly in both cases.
MEASUREMENT
Create a spark record for each of the two pairs of contact surfaces. Make sure you measure and record the mass of the disk and object A (with uncertainties).
ANALYSIS
From your two spark tapes, determine the accelerations. Remember, finding accelerations is NOT the purpose of this problem. Be sure to use an analysis technique that makes the most efficient use of your data and your time. What is the minimum number of spark dots you need to analyze to determine an acceleration accurately and reliably?
For each pair of contact surfaces, calculate the kinetic frictional force using the equation you obtained from answering the Method Questions.
What does your data show is the effect of the contact surfaces? What can you say about the magnitude of the kinetic frictional force when the contact surfaces are the same?
CONCLUSION
Which surfaces, laminate on laminate or composition board on composition board, will you recommend your friend to use for the game? Why? State your result in the most general terms supported by your analysis. Did your measurements agree with your initial prediction? If not, why?
PROBLEM #2: FORCES IN EQUILIBRIUM
You have a summer job with a University of Minnesota research group studying the ecology of a rain forest in South America. To get around the rain forest, the team members walk along a nylon-rope walkway that the local inhabitants have strung in a long line from tree to tree through the forest canopy. Your supervisor is concerned about the maximum amount of equipment each team member should carry to safely walk from tree to tree. If the walkway sags too much, the team member could be in danger, not to mention possible damage to the rain forest. Your supervisor knows you have taken physics, so she asks you to solve the problem.
You begin by assuming there is a constant force on both ends of each section of the walkway, where the line is held up by the trees. You need to determine how the sag of the walkway is related to the mass of a team member plus equipment when they are at the center of the walkway between two trees. To check your calculation, you decide to model the situation using the equipment shown below.
 |
How does the vertical displacement of an object
suspended on a string halfway between two pulleys, depend
on the mass of that object? |
EQUIPMENT
The system consists of a central object, B, suspended halfway between two pulleys by strings. The picture below is similar to the situation with which you will work.
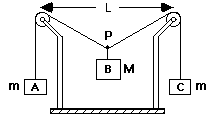
The objects A and C, which have the same mass, allow you to determine the force exerted on the central object by the string if you assume that the pulleys are frictionless and the strings are massless. A ruler and additional weights are provided for this investigation.
PREDICTION
Predict quantitatively the change in the vertical displacement of the central object (B) as you increase its mass. You should obtain an equation which predicts how the vertical displace-ment of central object B depends on its mass (M), the mass (m) of objects A and C, and the horizontal distance between the two pulleys (L).
Use your equation to sketch the expected shape of the graph of the vertical displacement versus mass of object B.
METHOD QUESTIONS
This experimental problem is similar to problems at the end of Chapter 4 of your text (for example, problem 43). The best way to solve this problem is to use a problem-solving strategy such as the one outlined in your text on pages 35:
1. Draw a sketch similar to the one in the Equipment section. Show how the vertical displacement of object B is related to the angle that the string stretched between the two pulleys sags below the horizontal.
2. The "known" (measurable) quantities in this problem are L, m and M; the unknown quantity is the vertical displacement of object B.
3. Use Newton's laws to solve this problem. Draw separate force diagrams for objects A, B, C and for point P. (If you need help, see pages 107 and 110 of your text.)
Which angles between your force vectors and your horizontal coordinate axis are the same as the angle between the strings and the horizontal?
4. For each force diagram, write Newton's second law and the corresponding equation of motion for each mass. What special condition applies to this problem? (If you need help, see page 134.)
5. Solve your equations for the vertical displacement. Your final equation predicts how the vertical displacement of object B depends on its mass (M), the mass (m) of objects A and C, and the horizontal distance between the two pulleys (L).
Now you can make your prediction for this problem: Use your equation to sketch the shape of a graph of the vertical displacement versus mass of object B.
EXPLORATION
Start with just the string suspended between the pulleys (no central object), so that the string looks horizontal. Attach a central object and observe how the string sags. Decide on the origin from which you will measure the vertical position of the object.
Try changing the mass of objects A and C (keep them equal for the measurements but you will want to explore the case where they are not equal).
Do the pulleys behave in a frictionless way for the entire range of weights you will use? How can you determine if the assumption of frictionless pulleys is a good one?
Add mass to the central object to decide what increments of mass will give a good range of values for the measurement.
MEASUREMENT
Measure the vertical position of the central object as you increase its mass. Make a table and record your measurements.
ANALYSIS
Make a graph of the vertical displacement of the central object as a function of its mass. On the same graph, plot your predicted equation for vertical displacement versus mass of the central object.
What are the limitations on the accuracy of your measurements and analysis? Over what range of values do the two curves match the best? Where do the two curves start to diverge from one another? What does this tell you about the system?
CONCLUSION
What will you report to your supervisor? How does the vertical displacement of an object suspended on a string between two pulleys depend on the mass of that object? Did your measurements of the vertical displacement of object B agree with your initial predictions? If not, why? State your result in the most general terms supported by your analysis.
What information would you need to apply your calculation to the walkway through the rain forest?
Check Your Understanding:
Estimate reasonable values for the information you need, and
solve the problem for the walkway over the rain forest.
PROBLEM #3: NORMAL FORCE AND THE KINETIC FRICTIONAL FORCE (PART A)
You are working for a company that contracts to test the mechanical properties of different materials or systems. One of the customers wants your group to determine the coefficient of kinetic friction for a new material made from recycled wood. They give you a sample of the material to use in your test.
You decide to measure the coefficient of friction by graphing the frictional force versus the normal force using a disk and ramp made from the sample of the material Of course, there is experimental measurement uncertainty no matter how you make the measurement. So you decide to vary the normal force in two different ways to see if you get consistent results. You divide your group into two teams. One team will vary the normal force by changing the angle of incline of the ramp (Problem #4). Your team will vary the normal force by changing the mass of the disk.
| |
What is the coefficient of kinetic friction of the
material? Which method of changing the normal force
yields the best results? |
EQUIPMENT
A wooden disk slides down a ramp, as shown below.
The tilt of the ramp with respect to the horizontal can be adjusted. You can change the mass of the disk by attaching weights to it. A spark tape running through a spark timer allows you to record the motion of the disk as it slides down the ramp.
PREDICTIONS
Examine the Table of Coefficients of Friction. Make your best guess of what you think the approximate value will be for the coefficient of friction of the material. Explain your reasoning.
Make a sketch of what you expect the graph of the magnitude of the kinetic frictional force versus the magnitude of the normal force to look like.
Do you expect the kinetic frictional force on the disk to increase, decrease, or stay the same as the normal force on the disk increases? Explain your reasoning.
METHOD QUESTIONS
To test your prediction you must determine how to calculate the normal force and the kinetic frictional force from the quantities you can measure in this problem. It is useful to have an organized problem-solving strategy such as on page 35 (and 107, 110) in your text:
1. Make a sketch of the problem situation similar to the one in the Equipment section. What measurements could you make with a meter stick to determine the angle of incline?
2. Draw a force diagram of the disk as it slides down the ramp. What is the reason for using the coordinate system you picked? What angles between your force vectors and your coordinate axes are the same as the angle between the ramp and the table?
3. Apply Newton's second law in the direction for which there is no acceleration. Determine an equation for the magnitude of normal force on the disk as a function of its mass and the angle of incline of the ramp. In this problem, you will change the normal force on the disk by changing its mass (keeping the angle of incline constant).
4. Apply Newton's second law in the direction the disk accelerates. Determine an equation for the magnitude of the kinetic frictional force on the disk as a function of its mass, its acceleration, and the angle of the incline.
EXPLORATION
Find an angle at which the disk accelerates down the board. Try this for disks of several different masses.
Select an angle and series of masses that will make your measurements most reliable.
Keeping the board at the same angle, take a spark record of the disk's motion. Make sure you measure and record that angle. You will need it later.
Repeat this procedure for different masses. Make sure each new mass moves freely down the incline.
Analyze your data as you go along (before making the next spark tape) so you can determine how many spark tapes you need to make, and what the disk's mass should be for each tape. Collect enough data to convince yourself and others of your conclusion about how the kinetic frictional force on the disk depends on the normal force on the disk.
ANALYSIS
For each new disk mass and spark tape, calculate the magnitude of the kinetic frictional force and the normal force on the disk.
Graph the magnitude of the kinetic frictional force versus the magnitude of the normal force for one angle and the different masses you used. On the same graph, show your predicted relationship.
What are the limitations on the accuracy of your measurements and analysis? Over what range of values does the measured graph match the predicted graph best? Where do the two curves start to diverge from one another? What does this tell you about the system?
CONCLUSION
Does your measured value of the coefficient of friction for the material agree with your initial prediction? If not, why? State your result in the most general terms supported by your analysis.
If available, compare your value of the coefficient of kinetic friction (with uncertainty) with the value obtained by the other team. Are the values consistent? Which way of varying the normal force to measure the coefficient of friction do you think is better? Why?
Check Your Understanding:
Compare the value of the coefficient of friction (with
uncertainty) you measured in this problem with the coefficient
you measured in Problem #1. Are the values
consistent? Which way of measuring the coefficient of friction do
you think is better? Why?
PROBLEM #4: NORMAL FORCE AND THE KINETIC FRICTIONAL FORCE (PART B)
You are working for a company that contracts to test the mechanical properties of different materials or systems. One of the customers wants your group to determine the coefficient of kinetic friction for a new material made from recycled wood. They give you a sample of the material to use in your test.
You decide to measure the coefficient of friction by graphing the frictional force versus the normal force using a disk and ramp made from the sample of the material Of course, there is experimental measurement uncertainty no matter how you make the measurement. So you decide to vary the normal force in two different ways to see if you get consistent results. You divide your group into two teams. One team will vary the normal force by changing the mass of the disk (Problem #3). Your team will vary the normal force by changing the angle of incline of the ramp.
| |
What is the coefficient of kinetic friction of the
material? Which method of changing the normal force
yields the best results? |
EQUIPMENT
A wooden disk slides down a ramp, as shown below.
The tilt of the ramp with respect to the horizontal can be adjusted. You can change the mass of the disk by attaching weights to it. A spark tape running through a spark timer allows you to record the motion of the disk as it slides down the ramp.
PREDICTIONS
Examine the Table of Coefficients of Friction. Make your best guess of what you think the approximate value will be for the coefficient of friction of the material. Explain your reasoning.
Make a sketch of what you expect the graph of the magnitude of the kinetic frictional force versus the magnitude of the normal force to look like.
Does the kinetic frictional force on the disk increase, decrease, or stay the same as the normal force on the disk increases? Explain your reasoning.
METHOD QUESTIONS
To test your prediction you must determine how to calculate the normal force and the kinetic frictional force from the quantities you can measure in this problem. It is useful to have an organized problem-solving strategy such as on page 35 (and 107, 110) in your text:
1. Make a sketch of the problem situation similar to the one in the Equipment section. What measurements could you make with a meter stick to determine the angle of incline?
2. Draw a force diagram of the disk as it slides down the ramp. What is the reason for using the coordinate system you picked? What angles between your force vectors and your coordinate axes are the same as the angle between the ramp and the table?
3. Apply Newton's second law in the direction for which there is no acceleration. Determine an equation for the magnitude of normal force on the disk as a function of its mass and the angle of incline of the ramp. In this problem, you will change the normal force on the disk by changing the angle of incline of the ramp (keeping the mass of the disk constant).
4. Apply Newton's second law in the direction the disk accelerates. Determine an equation for the magnitude of the kinetic frictional force on the disk as a function of its mass, its acceleration, and the angle of the incline.
EXPLORATION
Find a mass for which the disk accelerates down the board. Try this for disks of several different masses and several different angles.
Select a disk mass which gives you the greatest range of angles.
MEASUREMENT
Keeping the disk mass constant, make a spark record of the disk's motion. Make sure you measure and record the mass and angle. You will need it later.
Repeat this procedure for different angles of incline of the ramp. Make sure the disk moves freely down each new incline.
Analyze your data as you go along (before making the next spark tape) so you can determine how many spark tapes you need to make, and what the disk's mass should be for each tape. Collect enough data to convince yourself and others of your conclusion about how the kinetic frictional force on the disk depends on the normal force.
ANALYSIS
For each new angle of incline and spark tape, calculate the magnitude of the kinetic frictional force and the normal force on the disk.
Graph the magnitude of the kinetic frictional force versus the magnitude of the normal force for the mass of the disk and the different angles you used. On the same graph, show your predicted relationship.
What are the limitations on the accuracy of your measurements and analysis? Over what range of values does the measured graph match the predicted graph best? Where do the two curves start to diverge from one another? What does this tell you about the system?
CONCLUSION
Does your measured value of the coefficient of friction for the material agree with your initial prediction? If not, why not? State your result in the most general terms supported by your analysis.
If available, compare your value of the coefficient of kinetic friction (with uncertainty) with the value obtained by the other team. Are the values consistent? Which way of varying the normal force to measure the coefficient of friction do you think is better? Why?
Check Your Understanding:
Compare the value of the coefficient of friction (with
uncertainty) you measured in this problem with the coefficient
you measured in Problem #1.
Are the values consistent? Which way of measuring the coefficient
of friction do you think is better? Why?
Table of Coefficients of Friction*
1. A cart and Block 1 are connected by a massless
string that passes over a frictionless pulley, as shown in the
diagram below.
When Block 1 is released, the string pulls the cart toward the
right along a horizontal table. For each question below, explain
the reason for your choice.
a. The speed of the cart is:
(a) constant.
(b) continuously increasing.
(c) continuously decreasing.
(d) increasing for a while, and constant thereafter.
(e) constant for a while, and decreasing thereafter.
b. The force of the string on Block 1 is
(a) zero.
(b) greater than zero but less than the weight of Block 1.
(c) equal to the weight of Block 1.
(d) greater than the weight of Block 1.
(e) It is impossible to tell without knowing the mass of Block 1.
c. When the cart traveling on the table reaches position x,
the string breaks. The cart then
(a) moves on at a constant speed.
(b) speeds up.
(c) slows down.
(d) speeds up, then slows down.
(e) stops at x.
d. Block 1 is now replaced by a larger block (Block 2) that
exerts twice the pull as was exerted previously. The cart
is again reset at starting position xo and released. The string
again breaks at position x. Now, what is the speed of the
cart at position x compared to its speed at that point
when pulled by the smaller Block 1?
(a) Half the speed it reached before.
(b) Smaller than the speed it reached before, but not half of it.
(c) Equal to the speed it reached before.
(d) Double the speed it reached before.
(e) Greater than the speed it reached before, but not twice as
great.
2. A crate is given an initial push up the ramp of a large
truck. It starts sliding up the ramp with an initial velocity vo,
as shown in the diagram below. The coefficient of kinetic
friction between the box and the floor is uk.
Will the magnitude of the acceleration of the sliding crate be greater on the way up or on the way back down the ramp? Or will the accelerations be the same? Explain using appropriate force diagrams.
3. The same constant force (P) is applied to three identical boxes that are sliding across the floor. The forces are in different directions, as shown in the diagram below.
On which of the three boxes is the frictional force the largest? The smallest? Or is the frictional force on each box be the same? Explain using appropriate force diagrams and Newton's second law.
4. A lamp is hanging from two light cords. The cords make
unequal angles with the ceiling, as shown in the diagram.
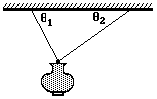
a. Draw the force diagram of the lamp. Clearly describe each
force drawn.
b. Is the horizontal component of the pull of the left cord on
the lamp greater than, less than, or equal to the horizontal
component of the pull of the right cord on the lamp? Explain your
reasoning.
c. Is the vertical component of the pull of the left cord on the
lamp greater than, less than, or equal to the vertical component
of the pull of the right cord on the lamp? Explain your
reasoning.
d. Is the vertical component of the pull of the left cord on the
lamp greater than, less than, or equal to half the weight of the
lamp? Explain your reasoning.
Check Your Understanding: